7.3 Calculation Examples of rectangular compression springs
Table 12-2-38
| Projet | Unit | Formulas and data | |
| Original condition | Outer diameter D2 | mm | 48 |
| Maximum working load Pn | N | 1500 | |
| Deformation under maximum working load Fn | mm | 35.2 | |
| Load class | Class II | ||
| End structure | The end of the compression spring is tight and smooth, and the supporting ring is 1 circle | ||
| Calculation item | Select material and allowable stress τp | MPa | Select material 60Si2Mn, according to Class II load, refer to Table 12-2-2 to obtain: G=79×103MPa According to Table 12-2-6, τp =590MPa |
| Choose the winding ratio C | Chooce C=5 | ||
| Calculate side length a and side length b | mm | take a>b,and choose a/b=1.25,so b/a=0.8 a=D2/(C+1)=48/(5+1)=8 b=b/a*a=0.8*8=6.4 |
|
| Spring pitch diameter D Spring inner diameter D1 |
D=D2-a=48-8=40 D1=D2-2a |
||
| Check the shear stress τ | MPa | In Figure 12-2-12, a/b=1.25 and C=5 give β value of 2.9. So,τ=βPn*D/ab√ ab=2.9(1500*40)/8*6.4√ 8*6.4=475<τp=590 The seems meets the requirements |
|
| Effective coils n | coil | In Figure 12-2-12, a/b=1.25 and C=5 give γ value of 5.6 n=Ga2*b2Fn/γPD3=7.9*104*82*6.42*35.2/(5.6*1500*403)=13.59 take n=13.60 |
|
| Total coils n1 | coil | As shown in Table 12-2-36, n1=n+2=13,6+2=15.6 | |
| Spring stiffness P ‘ | N/mm | P‘=Ga2*b2/γD3n=79*104*82*6.42/5.6*403*13.6=42.5 | |
| Working ultimate load Pj | N | According to table 12-2-36,take τj=1.25τp so, Pj=ab√ ab/βDTj=2347 |
|
| Deformation under working ultimate load Fj | mm | Fj=Pj/P ‘=2347/42.5=55.22 | |
| Minimum working load P1 | N | P1=1/3Pj=1/3*2347=782 | |
| Deformation under minimum working load F1 | mm | F1=P1/P ‘=782/42.5=18.4 | |
| Working Stroke h | mm | h=Fn– F1= 35.2-18.4=16.8 | |
| Pitch t | mm | take t=0.3D=0.3*40=12 | |
| Spacing δ | mm | δ=t-b=12-6.4=5.6 | |
| Free height H0 | mm | According to table 12-2-36, H0=nt+1.5b=13.6*12+1.5*6.4=172.8 | |
| Pressing height Hb | mm | According to table 12-2-36, Hb=(n+1.5)b=(13.6+1.5)*6.4=97 |
|
| Helix angle α | (°) | α=arctant/πD=5.46°=5°28′ | |
| Extension Length L | mm | L=n1πD=15.6*3.14*40=1959 | |
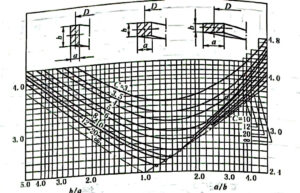
Figure 12-2-12 β values of coefficients





