2. Classification of truncated conical coil springs
Truncated conical coil springs can be divided into two types: equal pitch type and equal helical rise Angle type. The cross-section of their material is circular.
(1) Conical coil spring with equal pitch (Figure 12-3-2)
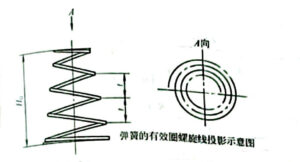
Figure 12-3-2 Equal pitch truncated conical coil spring
The axis of its spring wire is a spatial helix, and the projection of this helix on the supporting surface perpendicular to the conical center line formed by it is an Archimedean helix, and its mathematical expression is:
R=R1+(R2-R1)θ/2πn
Where R- the radius of curvature of any point on the spring wire;
R1- the curvature radius of the small end of the spring wire;
R2- the curvature radius of the large end of the spring wire;
θ- The Angle (radian) between the starting point and any point on the spring wire from the small end R of the spring wire;
n- Number of working cycles of the spring.
(2) Equal helical rise Angle truncated conical helical spring (Figure 12-3-3)
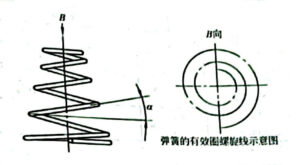
Figure 12-3-3 equal-helical Angle truncated cone helical spring
Its spring wire axis is a spatial helix, and the projection of this helix on the supporting surface perpendicular to the conical center line formed by it is a logarithmic helix, and its mathematical expression is as follows:
R=R1emθ
m=1nR2/R1 2*1/2πn
Where R is the curvature radius of any point on the spring wire;
R1- the curvature radius of the small end of the spring wire;
R2 – the curvature radius of the large end of the spring wire;
θ- The Angle (radian) between the small end R of the spring wire and any point on the spring wire:
n- Number of working cycles of the spring.
The spiral Angle of a conical spring is a constant, and the pitch of each spring ring is a variable. The surface formed by the rotation of the spring wire around the spring axis is a conical surface.





