Calculation Example of Cylindrical Helical Tension Spring

4.2 Calculation Example of Cylindrical Helical Tension Spring

Table 12-2-26 Calculation Example of Cylindrical Helical Tension Spring 1

Items		Unit	Formulas and Data
Original condition	Maximum tension P_n Minimum tension P₁ Working range h Spring external diameter Number of load actions N Spring material End structure	N N mmmm	350 176 12 ≤18 N<10³times Carbon spring steel wire, grade C Circular hook ring compression center
Parameter calculation	Initial calculation of spring stiffness P’	N/mm	P’=(P_n-P₁)/h=(350-176)12=14.5
	Minimum working load of the spring P₁	N	As it is a Class III load, P_j≥P_n Considering that it is a tension spring, P_j in Table 12-2-19 should be multiplied by 0.8 times. For direct table lookup, change to P. Divide by 0.8,Namely:P_j=P_n1/0.8=3501/0.8=440
	Material diameter d and spring pitch diameter D	mm	Refer to Table 12-2-19 and select d=3,D=14,P_j=444.99,f_j=1.527,P’_d=291,P_o=97.4
	Effective coils n	coil	n=P_d‘/P’=291/14.5=20.06 take n=20
	Spring stiffness P’	N/mm	P’=P_d‘/n=291/20=14.55
	Deformation under minimum load F₁	mm	F₁=(P₁-P_o)/P’=(176-97.4)/14.55=5.4
	Deformation under maximum load F_n	mm	F_n=(P_n-P_o)/P’=(350-97.4)/14.55=17.36
	Deformation under ultimate load F_j	mm	F_j=f_jn0.8=1.527200.8=24.43
	Spring outer diameter D₂	mm	D₂=D+d=14+3=17
	Spring inner diameter D₁	mm	D₁=D-d=14-3=11
	Free height H₀	mm	H₀=(n+1.5)d+2D=(20+1.5)d+2*14=92.5
	Length under minimum load H₁	mm	H₁=H₀+F₁=92.5+5.4=97.9
	Length under maximum load H_n	mm	H_n=H₀+F₂=92.5+17.36=109.86
	Length under service limit load Hj	mm	Hj=H₀+F_j=92.5+24.43=116.93
	Expanded length L	mm	L=πDn+2πD=3.141420+23.1414=967.12
Checking calculation	Actual limit deformation	mm	F_n+P_o/P’=17.36+97.4/14.55=20.05<F_j(24.43)
Checking calculation	Actual limit load	N	P_j0.8=444.990.8=356>P_n(350)

Table 12-2-27 Calculation Example II of Cylindrical Helical Tension Spring

Items		Unit	Formulas and Data
Original condition	Maximum tension P_n Minimum tension P₁ Working range h Number of load applications Spring material End structure	N N mm mm times	340 180 11 ≤22 10³~10⁵ Oil quenched and tempered carbon spring steel wire Class B Round hook type
Parameter calculation	Initial spring stiffness P’	N/mm	P’=(P_n-P₁)/h=(340-180)11=14.5
	Working limit load P_j	N	Because it is a class II load, P_j ≥ 1.25P_n, take P_j=1.25P_n=1.25 ×340=425, but considering the tension spring, the value of P_j in Table 12-2-19 should be multiplied by 0.8. In order to directly look up the table, divide 425 by 0.8, then P_j =405×1/0.8=531.25
	Spring material diameter d and spring diameter D	mm	According to Table 12-2-19, d=3.5, D=18, P_j =564.41,f_j=2.221, P’_d=254, P_o= 109。 As the spring material is oil quenched and tempered carbon spring steel wire B,thus δb=1569 Now, P_j =564.41 and f_j=2.221 obtained from Table 12-2-19 are corrected according to Table 12-2-18 P_j =1569/1570564.41=564 f_j=511569/0.7910⁵2.221=2.250
	Effective turns n	coils	n=P_d‘/P’=254/14.5=17.5 take n=18
	Spring stiffness P ‘	N/mm	P’=P_d‘/n=254/18=14.11
	Deformation under minimum load F₁	mm	F₁=(P₁-P_o)/P’=(180-109)/14.11=5.03
	Deformation under maximum load F_n	mm	F_n=(P_n-P_o)/P’=(340-109)/14.11=16.37
	Deformation under ultimate load F_j	mm	F_j=f_jn0.8=2.250180.8=32.4
	Spring outer diameter D₂	mm	D₂=D+d=18+3.5=21.5
	Spring inner diameter D₁	mm	D₁=D-d=18-3.5=14.5
	Free height H₀	mm	H₀=(n+1.5)d+2D=(18+1)×3.5+2×18=102.5
	Length under minimum load H₁	mm	H₁=H₀+F₁=102.5+5.03 =107.53
	Length under maximum load H_n	mm	H_n=H₀+F₂=102.5+16.37=118.87
	Length under service limit load Hj	mm	Hj=H₀+F_j=102.5+32.4=134.9
	Helix angle α	(°)	α=arctan t/πD=3.5/3.14*18=3.54 t=d=3.5mm
	Spring expansion length L	mm	L=πDn₁+2πD3/4=3.141818+23.14183/4=1102
Elastic property checking calculation	Actual limit deformation	mm	(P_o/P’+F_n)1.25=(109/14.11+16.37)1.25=30.111<F_j(32.4)
	Maximum working load P_n	N	P_n=P_o+P’*F_n=109+14.11×16.37=339.9≈340
	Actual limit load P_j	N	P_j*0.8=564×0.8=451.53>1.25×340 Namely, 451.53>425
Working drawing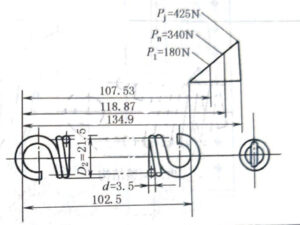