Calculation of cylindrical helical compression spring

Table 12-2-21 Calculation example of cylindrical helical compression spring 1

Items

Unit

Formulas and Data

Original condition

Minimum working load P₁
Maximum working load P_n
Working range h
Spring outside Diameter D₂
Spring Type
End Type
Spring Material

N
N
mm
mm

P₁=60

P_n=240

h=36±1

D₂≤45

N=10³~10⁶ times

The ends are tightened and ground, and the support rings at both ends are 1 circle each

Carbon Spring Wire Grade C

Parameter calculation

Initial spring stiffness P’

N/mm

P’=(P_n-P₁)/h=（210-60)/36=5

Working limit load P_j

Because it is a Class Ⅱ load: P_j≥1.25P, so P_j=1.25×240=300

Spring material diameter d and spring diameter D and related parameters

According to P_jand D conditions from Table 12-2-19:

d	D	P_j	f_j	P_d
3.5	38	306.97	11.37	27

Effective Coins n

Coin

n=P_d‘/P’=27/5=5.4

According to Table 12-10, take the standard value n=5.5

Total Coins n₁

Coin

n₁=n+2=5.5+2=7.5

Spring rate P’

N/mm

P’=P_d‘/n=27/5.5=4.9

Deformation under working limit load F_j

F_j=nf_j=5.5*11.37≈63

Pitch t

t=F_j/n+d=63/5.5+3.5=14.95

Free height H₀

H₀=nt+1.5d=5.5*14.95+1.5*3.5=87.47,take standard value H₀=90

Spring Outside diameter D₂

D₂=D+d=38+3.5=41.5

Spring inner diameter D₁

D₁=D-d=38-3.5=34.5

Helix angle α

(°)

α=arctan t/πD=arctan 14.95/π*38=7.14

Expanded length L

L=πDn₁/cosα=π*38*7.5/cos7.14=902

Height at minimum load H₁

H₁=H₀-P₁/P’=90-60/4.9=77.76

Height at maximum load H_n

H_n=H₀-P_n/P’=90-240/4.9=41.02

Height at ultimate load Hj

Hj=H₀-P_j/P’=90-306.97/4.9=27.35

Actual work range h

h=H₁-H_n=77.76-41.02=36.74≈36±1

Work area scope

P₁/P_j=60/306.97≈0.2；P_n/P_j=240/306.97≈0.8

Height to diameter ratio b

b=H₀/D=90/38=2.37＜2.6

Woring Drawing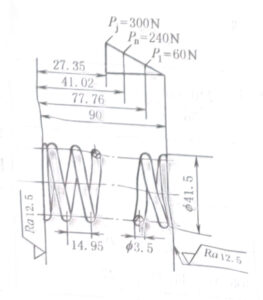

Calculation of cylindrical helical compression spring

skills requirement
1. Rotation: right-hand
2. Effective coins n=5.5, total coins n₁=7.5
3. Expanded length L=902mm
4. The accuracy requirements are not specified according to CB1239.2-2 level
5. The spring is treated with stress relief and tempering

Table 12-2-21 Calculation example of cylindrical helical compression spring 2

Name		Unit	Formulas and Data
Original condition	Maximum working load P_n Minimum working load P₁ Spring diameter D Working range h	N N mm mm	P_n=420 P₁=200 D=32 h=10
Original condition	Spring Category – Valve Spring Camshaft speed n_max Material End type	r/min	Class Ⅱ Spring,N=10³~10⁶ times Oil quenched and tempered carbon steel spring wire is used for the valve, both ends are tightened and ground flat, and the number of supporting rings is 1
Parameter calculation	Allowable stress τ_p	MPa	According to table 12-2-4，σ_b=1422,so τ_p=0.4,σ_b=568.8
	Initial C and K		According to the formula,8/πKC³=τ_pD₂/P_n=568.8*32²/420=1386.7
	Material diameter d	mm	d=D/C=32/7.7=4.16, take d=4.5
	Determine the winding ratio C		C=D/d=32/4.5=7.1
	Determine the curvature coefficient K		K=(4c-1)/(4C-4)+0.615/C or check table 12-2-20 K=1.21
	Spring stiffness P’	N/mm	P’=(P_n-P₁)/h=(420-200)10=22
	Deformation under minimum working load F₁	mm	F₁=P₁/P’=200/22=9.1
	Deformation under maximum working load F_n	mm	F_n=P_n/P’=420/22=19.1
	Deformation f during compaction F_b	mm	According to the stipulation that the working area of the compression spring should be 20% – 80% of the total deformation, take F_n=0.65F_b,So F_b=F_n/0.65=29.4
	Compression load P_b	N	According to the same provisions of the above item,P_b=P_n/0.65=420/0.65=646
	Effective Coins n	Coil	n=Gd⁴F_n/8P_nD³=79004.5⁴19.1/842032³=5.63,take n=6
	Total Coins n₁	Coil	According to table 12-2-14,n₁=n+2=6+2=8
	Pressing height H_b	mm	According to table 12-2-14,H_b=(n+1.5)d=(6+1.5)*4.5=33.75
	Free height H₀	mm	H₀=H_b+ F_b=33.75+29.4=63.15, take H₀=65
	Pitch t	mm	According to table 12-2-8,t=(H₀-1.5d)/n=(65-1.5*4.5)/6=9.71
	Helix angle α	(°)	α=arctan t/πD=arctan 9.71/3.14*32=5.52°
	Expanded length L	mm	L=πDn₁/cosα=π328/cos5.52°=808
	Pulsating fatigue limit τ₀	Mpa	According to table 12-2-16,when N=10⁷,τ₀=0.3σ_b=0.3*1422=420
	Minimum shear stress τ_min	Mpa	τ_min=8KDP₁/πd³=81.2132200/3.144.5³=216
	Maximum shear stress τ_max	Mpa	τ_max=8KDP_n/πd³=81.2132420/3.144.5³=454
	Fatigue safety factor s		S=(τ₀+0.75τ_min)/τ_max=(420+0.75*216)/454=1.28 S≈S_p=1.3-1.7
	Spring natural frequency f	1/s	f=3.5610⁵d/nD²=3.5610⁵4.5/6*32²=260.7
	Forced vibration frequency f_r	1/s	f_r=n_max/60=1400/60=23.3
	Resonance checking calculation f>10 f_r，namely 260.7>10×23.3