Calculation Formula of Cylindrical Helical Tension Spring

4.1 Calculation Formula of Cylindrical Helical Tension Spring

Table 12-2-25

Item		Unit	Formulas and data
Main calculation formula	Material Diameter d	mm	d≥1.6√￣P_n KC/τ_pIn the formula, τ_pis the allowable shear stress, which is selected as per Table 12-2-6 according to Class I, II and III loads K=(4C-1)/(4c-4)+0.615/C or Select according to Table 12-2-20
	Effective coils n	Coil	n=Gd⁴F_n/8(P_n-P₀)D³=GDF_n/8(P_n-P₀)C⁴ In the formula, P₀– initial tension, which can be found in Table 12-2-19
	Spring stiffness p‘	N/mm	P’=Gd⁴/8D³n=GD/8C⁴n,or P’=(P_n-P₁)/h
	Spring pitch diameter D	mm	Estimate according to the structural requirements, and then take the standard value
	Spring inner diameter D₁	mm	D₁=D-d
	Spring outer diameter D₂	mm	D₂=D+d
	Total coils n₁	Coil	n₁=n,When n>20, the circle is rounded to an integer. When n<20, round to half a circle
	Pitch t	mm	t=d+δ Take δ=0 for the compact coil spring
	Spacing δ	mm	δ=t-d
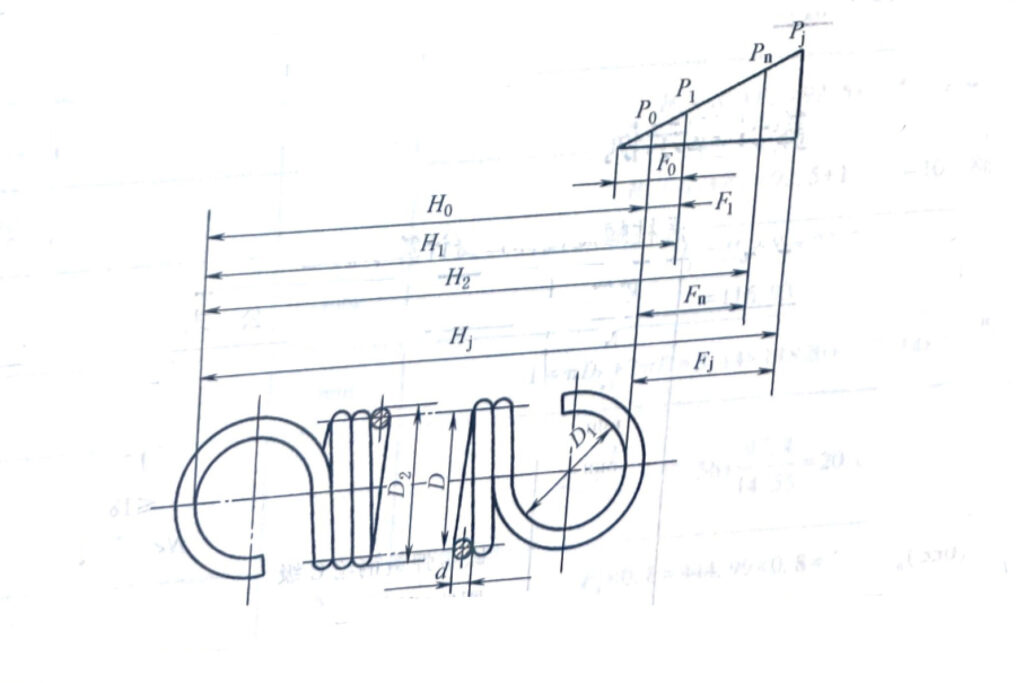
	Free height H₀	mm	LI Ho=(n+1)d+D LⅡ Ho=(n+1)d+2D LⅢ Ho=(n+1.5)d+2D
	Height at minimum load H₁	mm	H₁=H₀-F₁,F₁=8P₁C⁴n/GD-F₀
	Height at maximum load H_n	mm	H_n=H₀-F_n,F_n=8P_nC⁴n/GD-F₀
	Height at ultimate load Hj	mm	Hj=H₀-F_j,F_j=8P_jC⁴n/GD-F₀
	Helix angle α	(°)	α=arctan t/πD
	Spring Extending length L	mm	L≈πDn₁+Hook Extending length